4. 진법 변환 (Base Conversion)
4-1. 10진법 수 N을 B진법으로 바꾸려면 N이 0이 될때 까지 나머지를 계속 구하면 됩니다.
예를 들어 11을 3진법으로 바꾸는 방법은
11/3 = 3 나머지는2
3/3 = 1 나머지는0
1/3 = 0 나머지는1
그래서 위로 보면
따라서 11은 3진법으로 102 입니다.
백준 진법 변환문제
10진법 수 N을 B진법으로 바꿔 출력하는 문제입니다.
https://www.acmicpc.net/problem/11005
11005번: 진법 변환 2
10진법 수 N이 주어진다. 이 수를 B진법으로 바꿔 출력하는 프로그램을 작성하시오. 10진법을 넘어가는 진법은 숫자로 표시할 수 없는 자리가 있다. 이런 경우에는 다음과 같이 알파벳 대문자를
www.acmicpc.net
입력 받은 두 수의 나머지를 보고
10보다 작으면 임의의 문자열에 바로 더해주고, 10보다 크면 10은 A, 11은 B..로 문자열에 더해줍니다.
그리고 변환하는 수를 0이 될 때 까지 반복하여 나눠주고
0이되면 반복을 끝내, 만든 문자열을 뒤집어 출력하면 됩니다.
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
int n, b;
cin >> n >> b;
string ans = "";
while(n > 0){
int r = n % b;
if ( r < 10 ){
ans += ('0' + r);
}
else {
r = r - 10 + 'A';
ans += r;
}
n /= b;
}
reverse(ans.begin(), ans.end());
cout << ans;
return 0;
}
4-2. 반대로 B진법 수 N을 10진법으로 바꾸려면 B^k를곱하면서 더해가면 됩니다.
예를들어 3진법 수 102는
(1 x 3^2) + (0 x 3^1) + (2 x 3^0)
= 11
이렇게 각 자리수에 진법의 각 자리 제곱수를 곱해서 더해줍니다.
4-3. 2진수 -> 8진수
2진수를 세 자리씩 묶어서 계산하면 됩니다.
예를들어 101110011은 세 자리씩 묶으면
101 110 011이고,
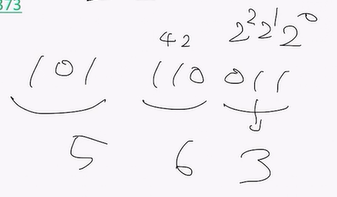
세 자리씩 더한값들을 연결하면
= 563 이 8진수가 됩니다.
8진수에서 2진수는 위와 반대로 구하면 됩니다.
만약 A진수를 B진수로 바꾸고자 하면
A진수 -> 10진수 -> B진수로 바꾸면 됩니다.
5. 소수 (Prime Number)
소수는 약수가 1과 자신밖에 없는 수를 의미합니다.
- N이 소수가 되려면, 2보다 크거나 같고, N-1보다 작거나 같은 자연수로 나누어 떨어지면 안된다.
- 1부터 100까지 소수
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
이제 소수를 판별하는 함수를 작성하면
bool prime(int n){
if (n < 2) {
return false;
}
for (int i =2; i <= n-1; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}이 방식은 시간 복잡도가 O(N)입니다.
그런데 이렇게 모든 약수를 검사한다면 시간이 오래걸리게 됩니다.
그래서 더 빠르게 검사하는 방법으로
어떤 수 N 은 항상 A x B로 나타낼 수 있는데
두 수중 적어도 하나는 루트 N보다 작거나 같습니다.
왜냐하면 만약 둘다 루트 N보다 크면 A x B 는 N보다 커집니다.
따라서 두 수 A, B의 차이가 가장 적은 경우는 루트 N이고 이 루트 N까지만 검사를 해보면
소수인지 아닌지 판별할 수 있습니다.
아래는 더 빠르게 소수를 판별하는 함수입니다.
bool prime (int n) {
if (n < 2) {
return false;
}
for (int i = 2; i * i <= n; i ++) { // i <= 루트 N을 양변을 제곱하여 i*i <= N로 표현
if (n % i == 0) {
return false;
}
}
return true;
}여기서 시간 복잡도는 O(루트 N)
N이 1억인 경우 처음 코드는 1억번, 위 코드는 1만법
따라서 위 방법이 더 좋은 방법이 됩니다.
백준 소수 찾기 문제
https://www.acmicpc.net/problem/1978
1978번: 소수 찾기
첫 줄에 수의 개수 N이 주어진다. N은 100이하이다. 다음으로 N개의 수가 주어지는데 수는 1,000 이하의 자연수이다.
www.acmicpc.net
입력으로 주어지는 N개의 소수 중에서 소수가 몇 개 인지 구하는 문제입니다.
이 문제에서 고려해야 할 점은 시간입니다.
- 어떤 수 N이 소수인지 아닌지 알아내는데 걸리는 시간 복잡도는 O(루트 N)이었다.
- 그러면 1부터 1,000,000까지 모든 소수를 구하는데 걸리는 시간 복잡도는?
- 각각의 수에 대해 소수인지 판별하고 그 각각은 O(루트N)이 걸린다.
- 수는 총 N개 이므로, O(N루트N)이 걸린다.
- 1,000,000 * 1,000 = 1,000,000,000 = 10억 = 10초로 너무 긴 시간이 필요하다.
따라서 이보다 더 빠른 방법을 찾아야합니다.
1부터 N까지 범위 안에 들어가는 모든 소수를 구하려면 에라토스테네스의 체를 사용합니다.
에라토스테네스의 체
에라토스테네스의 체 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다. 알고리즘[편집] 2부터 소수를 구하고자 하는 구간
ko.wikipedia.org
1. 2부터 N까지 모든 수를 써놓는다.
2. 아직 지워지지 않은 수 중에서 가장 작은 수를 찾는다.
3. 그 수는 소수이다.
4. 이제 그 수의 배수를 모두 지운다.
처음 지워지지 않은 수 중에서 가장 작은 수는 2입니다. 2는 소수이고 2의 배수를 모두 지웁니다.
다음은 3을 제외한 3의 배수를 모두 지웁니다. 이렇게 계속 반복하면 남은 수는 소수입니다.
int p[100]; // 소수 저장
int pn = 0; // 소수의 개수
bool c[101]; // 지워졌으면 true
int n = 100; // 100까지 소수
for (int i = 2; i <= n; i++) {
if (c[i] == false) {
p[pn++] = i;
g\for (int j = i * i; j <= n; j+=i) {
c[j] = true;
}
}
}이 경우 시간 복잡도는 O(N log log N)입니다.
'알고리즘 > 알고리즘' 카테고리의 다른 글
| [기초] 자료구조 / 그래프 (Graph) (0) | 2022.08.09 |
|---|---|
| [기초] 정렬(sort) 알고리즘 (0) | 2022.08.08 |
| [기초] 알고리즘 수학1 (0) | 2022.08.01 |
| [기초] 다이나믹 프로그래밍(Dynamic Programming, DP) (0) | 2022.07.27 |
| [기초] 자료구조 / 큐(queue)와 덱(deque), 문자열 (0) | 2022.07.26 |





댓글