그래프를 저장하는 방식에 대해 알아봅니다.
그래프의 표현
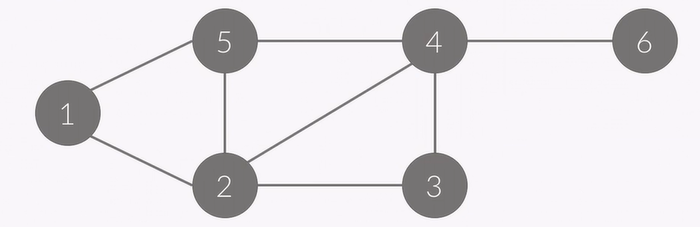
- 위와 같은 그래프는 정점이 6개, 간선이 8개 있다.
- 간선에 방향이 없기 때문에, 방향이 없는 그래프이다.
- 정점 : {1, 2, 3, 4, 5, 6}
- 간선 : {(1, 2), (1, 5), (2, 5), (2, 3), (3, 4), (2, 4), (4, 5), (4, 6)}
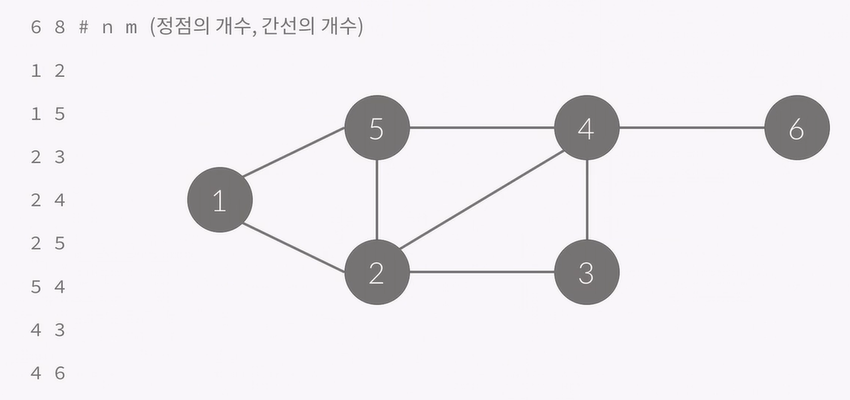
보통 위 그림과 같이 정점의 개수, 간선의 개수
그리고 m개의 줄에 어떤 간선이 연결되어 있는지 주어집니다.
인접 행렬(Adjacency-matrix)
정점의 개수를 V라 했을 때, V x V 크기의 이차원 배열을 이용합니다.
A[i][j] = 1 (i -> j 간선이 있을 때), 0 (없을 때)
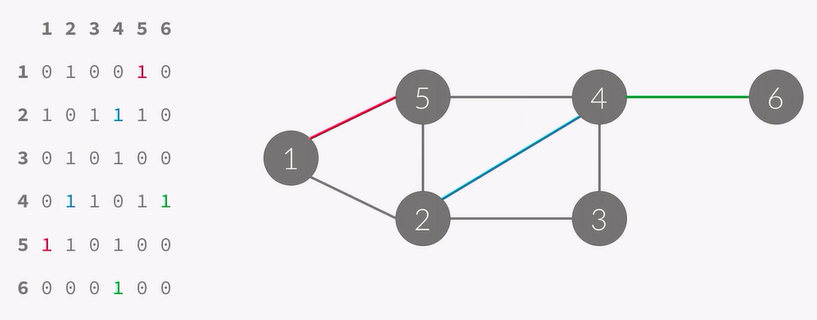
이 인접행렬은 없는 간선도 저장하기 때문에
불필요한 배열이 생겨 많이 사용하지 않는다고 합니다.
#include <cstdio>
#include <vector>
int a[10][10];
int main() {
int n, m;
scanf("%d %d", &n, &m);
for (int i= 0; i < m; i++){
int u, v;
scanf("%d %d", &u, &v);
a[u][v] = a[v][u] = 1;
}
}n은 정점개수 m은 간선개수(양방향 그래프이므로 맨 밑줄, 방향그래프면 a[v][u]가 없음)
이제 가중치가 있는 경우,
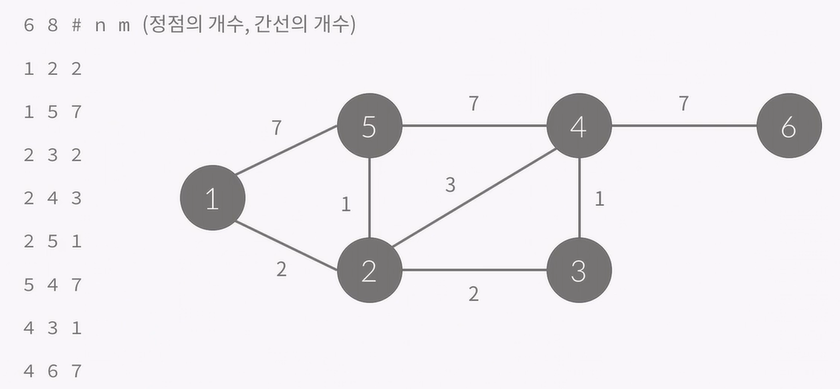
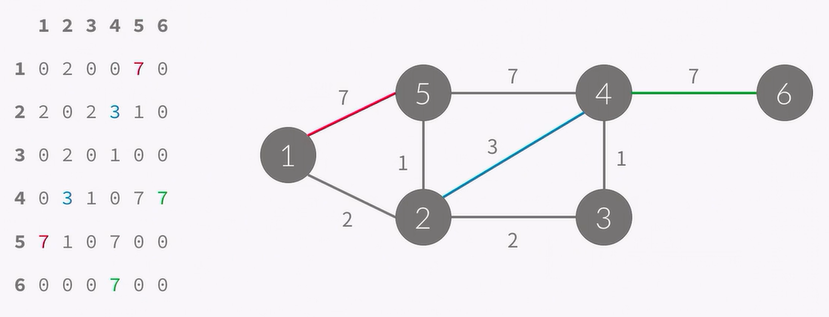
정점의 개수를 N이라 했을 때, N x N 크기의 이차원 배열을 이용합니다.
A[i][j] = w (i -> j 간선이 있을 때, 그 가중치), 0 (없을 때)
#include <cstdio>
#include <vector>
int a[10][10];
int main() {
int n, m;
scanf("%d %d", &n, &m);
for (int i= 0; i < m; i++){
int u, v, w;
scanf("%d %d %d", &u, &v, &w);
a[u][v] = a[v][u] = w;
}
}입력받을 때 가중치를 추가로 입력받습니다.
인접 리스트(Adjacency-list)
링크드 리스트를 이용해서 구현합니다.
A[i]= i와 연결된 정점을 링크드 리스트로 포함하고 있습니다.
링크드 리스트
연결 리스트 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org
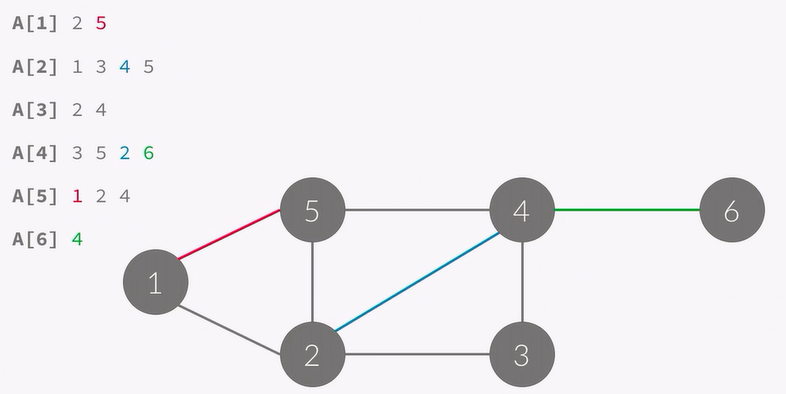
위 A[1]에 있는 2, 5는 정점이 아니라 간선이라는 점이 중요합니다.
인접 리스트를 사용하면 간선의 개수만큼만 저장하면 됩니다.
하지만 링크드 리스트는 구현하는데 시간이 오래걸리기 때문에, 주로 vector와 같이 가변적 배열을 이용해 구합니다.
#include <cstdio>
#include <vector>
using namespace std;
vector<int> a[10];
int main() {
int n, m;
scanf("%d %d", &n, &m);
for (int i= 0; i < m; i++){
int u, v;
scanf("%d %d", &u, &v);
a[u].push_back(v); a[v].push_back(u);
}
}
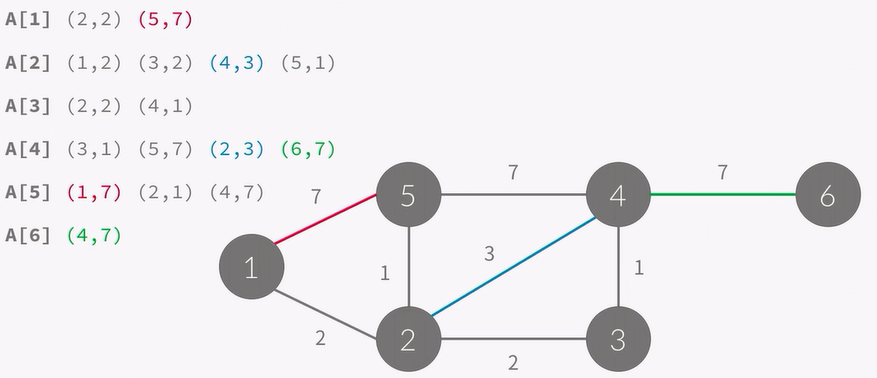
인접 리스트에서 가중치가 있는 경우, 간선에 가중치를 저장해야합니다.
#include <cstdio>
#include <vector>
using namespace std;
vector<pair<int><int>> a[10];
int main() {
int n, m;
scanf("%d %d", &n, &m);
for (int i= 0; i < m; i++){
int u, v, w;
scanf("%d %d %d", &u, &v, &w);
a[u].push_back(make_pair(v, w)); a[v].push_back((make_pair(u, w));
}
}
따라서 공간 복잡도는
- 인접 행렬 : O(V^2)
- 인접 리스트 : O(E)
간선 리스트(Edge-list)
인접 행렬이나 인접 리스트를 사용할 수 없는 경우(STL을 사용할 수 없는 경우 등) 사용합니다.
먼저 E라는 배열에 간선을 모두 저장합니다.
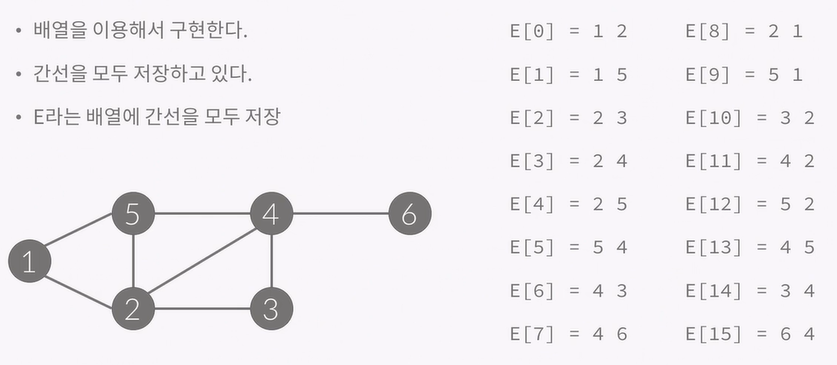
각 간선의 시작 정점을 정렬해줍니다.
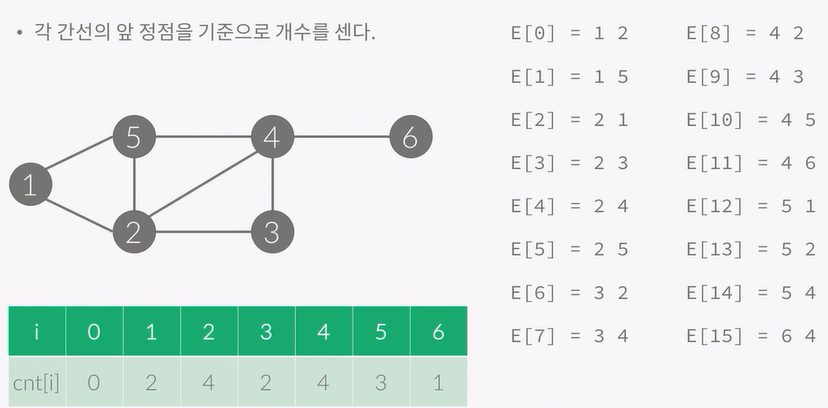
그리고 각 간선의 앞 정점을 기준으로 개수를 셉니다.
cnt배열의 누적합을 구합니다.

이 방법을 코드로 나타내면
for (int i = 0; i < m; i ++) {
cnt [e[i][0]] += 1;
}
for (int i = 1; i <= m; i ++) {
cnt[i] = cnt[i-1] + cnt[i];
}
이렇게 하면 i번 정점과 연결된 간선은 E배열에서 cnt[i -1]부터 cnt[i] -1 까지입니다.
그러므로 3번 정점과 연결된 간선은 cnt[2] ~ cnt[3] -1 즉, 6 ~7까지가 됩니다.
4번 정점은 cnt[3] ~ cnt[4] -1 즉, 8 ~ 11
이렇게 간선 리스트는 정렬만 구현이 잘 되면 사용할 수 있습니다.
공간 복잡도는 O(E)
그래프의 탐색
탐색은 두가지 종류가 있습니다.
목적은 모든 정점을 1번씩 방문하는 것 입니다.
DFS (Depth First Search)
깊이 우선 탐색 -> 최대한 깊숙히 많이 (스택 사용)
BFS (Breadth First Search)
너비 우선 탐색 -> 최대한 넓게 (큐 사용)
이때 모든 가중치가 1인 경우 최단 거리를 찾는 알고리즘은 BFS를 이용합니다.
깊이 우선 탐색 (DFS)
스택을 이용해서 갈 수 있는 만큼 최대한 많이 가고, 어디를 거쳐 갔는지 스택에 저장합니다.
갈 수 없으면 이전 정점으로 돌아갑니다.
모든 정점을 한 번씩 방문한다는 목적을 계속 생각하면 됩니다.
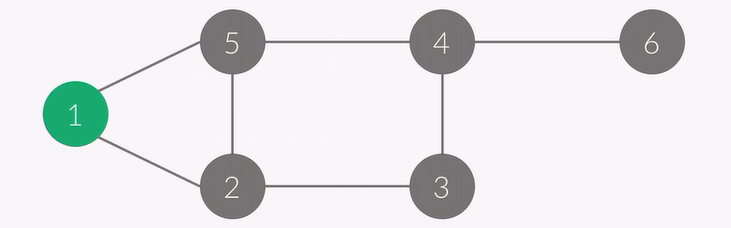
위와 같은 그래프에서 다음과 같이 정하고
현재 정점 : 1
순서 : 1
스택 : 1
아래와 같이 check[i] 배열을 만들어 0 또는 1을 저장합니다. (0은 아직 방문x, 1은 방문)

시작점인 1번 정점에서 갈 수 있는 경우는 2번과 5번이 있습니다.
이때 DFS에서는 아무 곳으로 가도 됩니다. 임의로 규칙을 정해서 낮은 정점으로 방문하기로 합니다.
그러면 2번을 방문하게 되고, check[2]는 1이되고 스택에도 2번이 들어가게 됩니다.
그러면
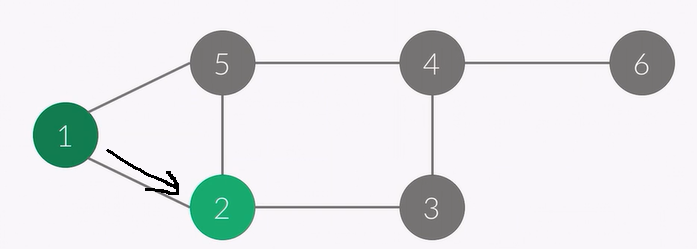
현재 정점 : 2
순서 : 1 2
스택 : 1 2
이후 check 배열은 아래 상태가 됩니다.

2번에서 갈 수 있는 경우는 3가지인데 1번은 이미 check되어 1이기 때문에 3으로 이동합니다.
현재 정점 : 3
순서 : 1 2 3
스택 : 1 2 3
이후 동일하게 3번에서 4번을 방문하고
현재 정점 : 4
순서 : 1 2 3 4
스택 : 1 2 3 4
5번을 방문하게됩니다.
현재 정점 : 5
순서 : 1 2 3 4 5
스택 : 1 2 3 4 5
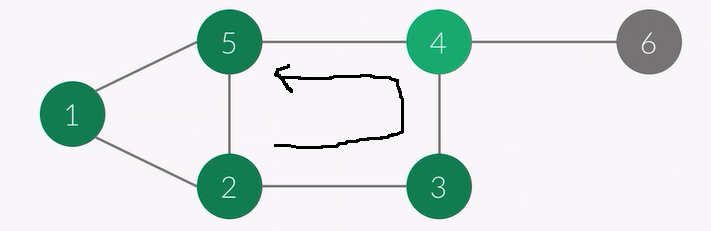
이후 check 배열은 아래 상태가 됩니다.

이제 5번에서는 1, 2, 4 로 방문 할 수 있는데 이미 방문 하여 더이상 갈 수 없습니다.
이때 스택에서 5를 하나 빼고 맨 위 값인 4로 돌아갑니다.
현재 정점 : 4
순서 : 1 2 3 4 5
스택 : 1 2 3 4
이제 4번에서는 6번으로 갈 수 있고 스택에 6번을 추가합니다.
현재 정점 : 6
순서 : 1 2 3 4 5 6
스택 : 1 2 3 4 6

check배열은 1로 다 바뀌었지만, 컴퓨터는 정점을 다 방문했는지 모르기 때문에
위 5번에서와 같이 스택을 pop연산 해주면서 비워갑니다.
현재 정점 : 4
순서 : 1 2 3 4 5 6
스택 : 1 2 3 4
pop연산으로 4를 지우고
현재 정점 : 3
순서 : 1 2 3 4 5 6
스택 : 1 2 3
...
...
...
현재 정점 :
순서 : 1 2 3 4 5 6
스택 :
이렇게 스택이 비어있는 상태가 되면 탐색을 종료합니다.
이제 DFS함수를 구현합니다. 재귀함수를 사용합니다. dfs(x)는 x를 방문했다는 의미
//인접 행렬을 이용한 구현
void dfs(int x) {
check[x] = true;
printf("%d", x);
for (int i = 1; i <= n; i++){
if (a[x][i] == 1 && check[i] == false){
dfs(i);
}
}
}//인접 리스트를 이용한 구현
void dfs(int x) {
check[x] = true;
printf("%d", x);
for (int i = 0; i < a[x].size; i++){
int y = a[x][i];
if (check[y] == false) {
dfs(y);
}
}
}
너비 우선 탐색 (BFS)
큐를 이용해서 지금 위치에서 갈 수 있는 것을 모두 큐에 넣는 방식입니다.
큐에 넣을 때 방문했다고 체크하면 됩니다.

위와 같은 그래프에서 다음과 같이 정하고
현재 정점 : 1
순서 : 1
큐 : 1

1에서 갈 수 있는 곳은 2와 5가 있기 때문에 큐에 둘다 넣고 check를 1로 바꿉니다.

그러면 다음과 같이 변합니다.
현재 정점 : 1
순서 : 1 2 5
큐 : 1 2 5
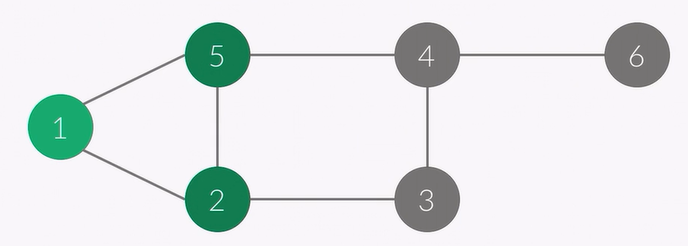
이제 1에서 갈 수 있는 곳이 더이상 없기 때문에 큐에서 하나를 pop하여 1이 빠집니다.
현재 정점 : 2
순서 : 1 2 5
큐 : 2 5
이제 2에서는 1, 3, 5로 갈 수 있는데 1, 5는 이미 방문하였기 때문에 큐에 3이 들어가고 check[3]은 1이 됩니다.
현재 정점 : 2
순서 : 1 2 5 3
큐 : 2 5 3

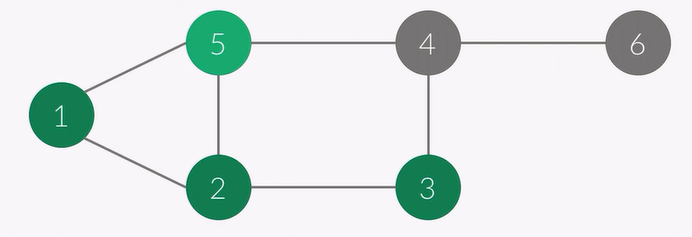
이제 2에서 갈 수 있는 곳이 더이상 없기 때문에 큐에서 하나를 pop하여 2이 빠집니다.
현재 정점 : 5
순서 : 1 2 5 3
큐 : 5 3
이제 5에서 1, 2, 4로 갈 수 있고 1, 2는 이미 방문 했으므로 4를 방문하고 check[4]=1, 그리고 큐에 넣습니다.
현재 정점 : 5
순서 : 1 2 5 3 4
큐 : 5 3 4

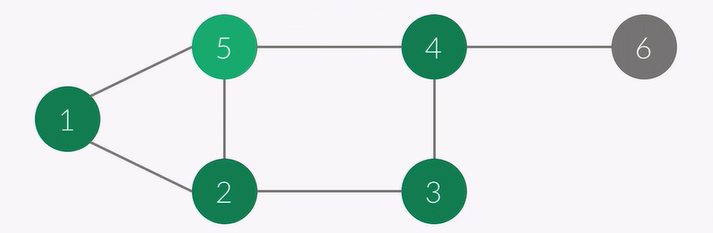
5번에서 더이상 방문할 수 있는 곳은 없기 때문에 3으로 넘어갑니다.
현재 정점 : 3
순서 : 1 2 5 3 4
큐 : 3 4
3번에서 더이상 방문할 수 있는 곳은 없기 때문에 4로 넘어갑니다.
현재 정점 : 4
순서 : 1 2 5 3 4
큐 : 4
4에서는 이제 6을 방문하고
현재 정점 : 6
순서 : 1 2 5 3 4 6
큐 : 4 6


현재 정점 : 6
순서 : 1 2 5 3 4 6
큐 : 6
현재 정점 :
순서 : 1 2 5 3 4 6
큐 :
6도 더이상 갈 수 있는 곳이 없으므로 큐에서 빠지게되고 탐색을 종료합니다.
BFS의 구현은 queue를 이용합니다.
//인접 행렬을 이용한 구현
queue<int> q;
check[1] = true; q.push(1);
while (!q.empty()) {
int x = q.front(); q.pop;
printf("%d", x);
for (int i = 1; i <= n; i++) {
if (a[x][i] == 1 && check[i] == false) {
check[i] = true;
q.push(i);
}
}
}//인접 리스트 이용한 구현
queue<int> q;
check[1] = true; q.push(1);
while (!q.empty()) {
int x = q.front(); q.pop;
printf("%d", x);
for (int i = 0; i < a[x].size(); i++) {
int y = a[x][i];
if (check[y] == false) {
check[y] = true; q.push(y);
}
}
}
백준 DFS와 BFS
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하는 문제입니다.
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
//인접 리스트 사용
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
using namespace std;
vector<int> a[1001];
bool check[1001];
void dfs(int node) {
check[node] = true;
printf("%d ",node);
for (int i=0; i<a[node].size(); i++) {
int next = a[node][i];
if (check[next] == false) {
dfs(next);
}
}
}
void bfs(int start) {
queue<int> q;
memset(check,false,sizeof(check));
check[start] = true;
q.push(start);
while (!q.empty()) {
int node = q.front();
q.pop();
printf("%d ",node);
for (int i=0; i<a[node].size(); i++) {
int next = a[node][i];
if (check[next] == false) {
check[next] = true;
q.push(next);
}
}
}
}
int main() {
int n, m, start;
scanf("%d %d %d",&n,&m,&start);
for (int i=0; i<m; i++) {
int u,v;
scanf("%d %d",&u,&v);
a[u].push_back(v);
a[v].push_back(u);
}
for (int i=1; i<=n; i++) {
sort(a[i].begin(), a[i].end());
}
dfs(start);
puts("");
bfs(start);
puts("");
return 0;
}// 간선 리스트 사용
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
struct Edge {
int from, to;
};
Edge edge[20001];
int cnt[1001];
bool check[1001];
bool cmp(const Edge &u, const Edge &v) {
if (u.from == v.from) {
return u.to < v.to;
} else {
return u.from < v.from;
}
}
void dfs(int node) {
check[node] = true;
printf("%d ",node);
for (int i=cnt[node-1]; i<cnt[node]; i++) {
int next = edge[i].to;
if (check[next] == false) {
dfs(next);
}
}
}
void bfs(int start) {
queue<int> q;
q.push(start);
check[start] = true;
while (!q.empty()) {
int node = q.front();
q.pop();
printf("%d ",node);
for (int i=cnt[node-1]; i<cnt[node]; i++) {
int next = edge[i].to;
if (check[next] == false) {
check[next] = true;
q.push(next);
}
}
}
}
int main() {
int n, m, start;
scanf("%d %d %d",&n,&m,&start);
for (int i=0; i<m; i++) {
scanf("%d %d",&edge[i].from, &edge[i].to);
edge[i+m].from = edge[i].to;
edge[i+m].to = edge[i].from;
}
m *= 2;
sort(edge, edge+m, cmp);
for (int i=0; i<m; i++) {
cnt[edge[i].from] += 1;
}
for (int i=1; i<=n; i++) {
cnt[i] += cnt[i-1];
}
dfs(start);
printf("\n");
memset(check,false,sizeof(check));
bfs(start);
printf("\n");
return 0;
}'알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] Isolation Forest (0) | 2023.05.09 |
|---|---|
| [기초] 자료구조 / 트리 (Tree) (0) | 2022.08.12 |
| [기초] 자료구조 / 그래프 (Graph) (0) | 2022.08.09 |
| [기초] 정렬(sort) 알고리즘 (0) | 2022.08.08 |
| [기초] 알고리즘 수학2 (0) | 2022.08.02 |





댓글